Patterns, Plans, and Iteration

Making a plan

You have just been randomly assigned to work with a partner – find them now.

The following T-shirt – available for purchase if you're interested – is offered without comment:

Have the planning sheet you were given ready:

With your partner, draw the design shown in this animation on your planning sheet:

Look for Patterns

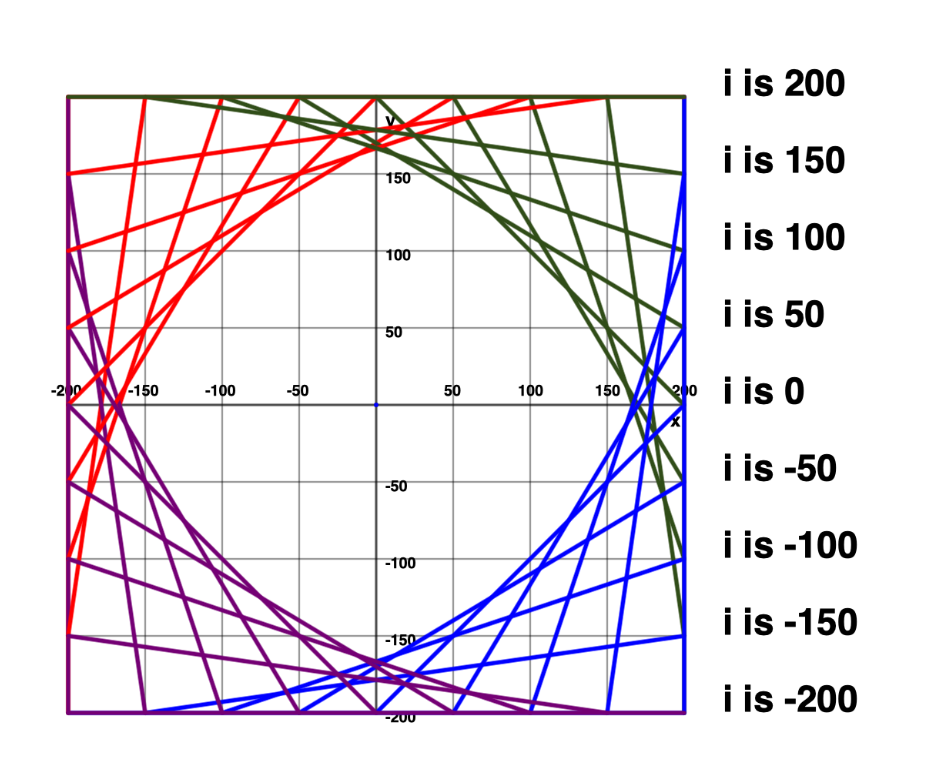
Assume that the lower left corner is at $(-200,-200)$.

Consider the start and end points for each line.

L👀K for patterns – what do you notice?

What changes?

What stays the same?

After examining start and end points:

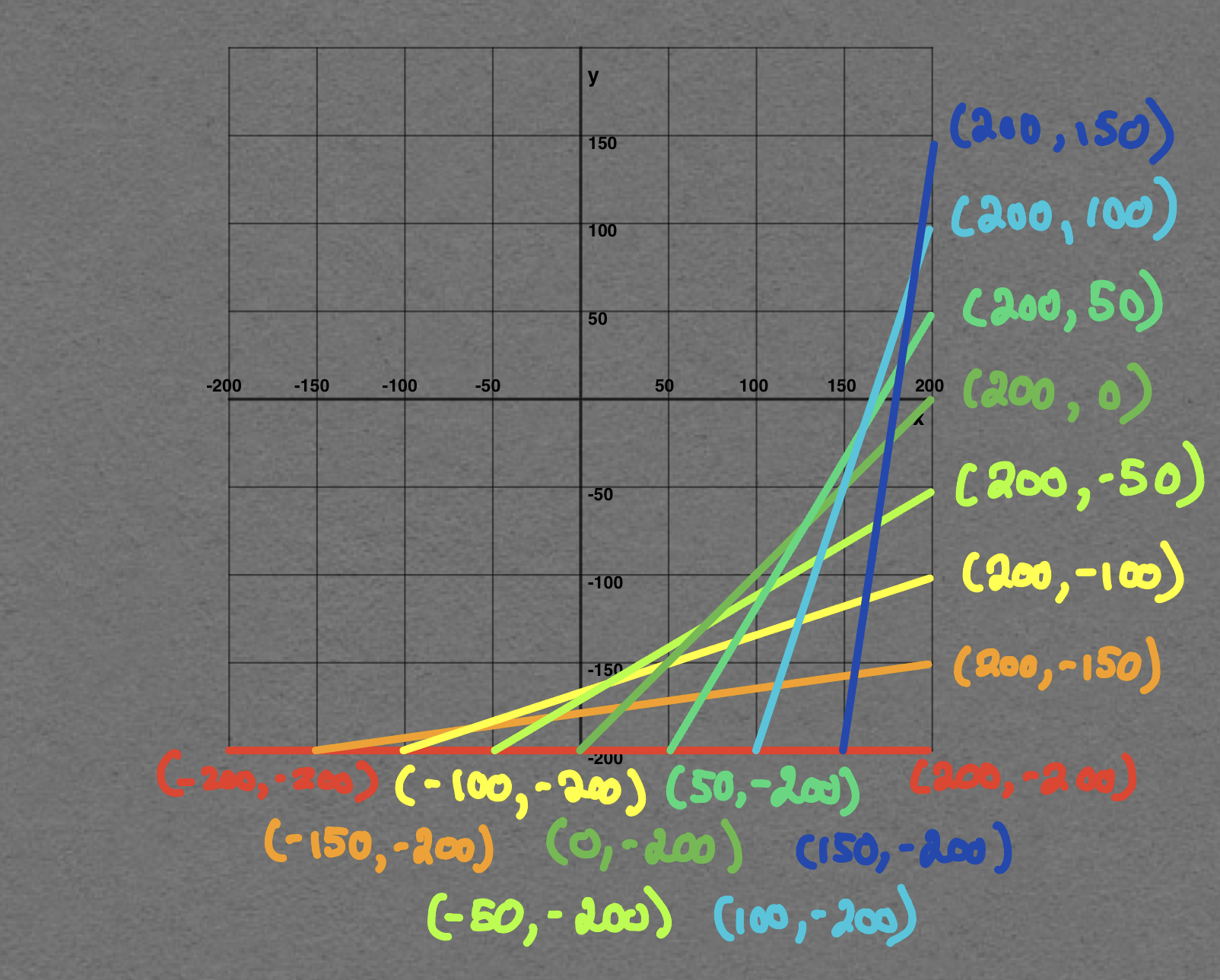
You may have noticed that:

• the $x$ position of the start of each line increases by 50 from one line to the next
• the $y$ position of the start of each line stays constant at -200

Likewise:

• the $x$ position of the end of each line stays constant at 200
• the $y$ position of the end of each line increases by 50 from one line to the next

Applying Iteration

We can use another form of a loop in Swift to express this kind of numerical pattern.

You already know how to express a loop that counts from 1 through 10:

for i in 1...10 {
	// code to repeat goes here
	// "i" begins at 1, changes to 2, then 3, then 4...
	// and ends at 10
}

To express a loop that counts from 2 through 10, by 2's, we would write:

for i in stride(from: 2, through: 10, by: 2) {
    // "i" begins at 2, changes to 4, then 6...
    // ending at 10
}

We can use that same type of syntax to express the pattern:

$-200,-150,-100...100,150,200$

... that we observed when making our plan.

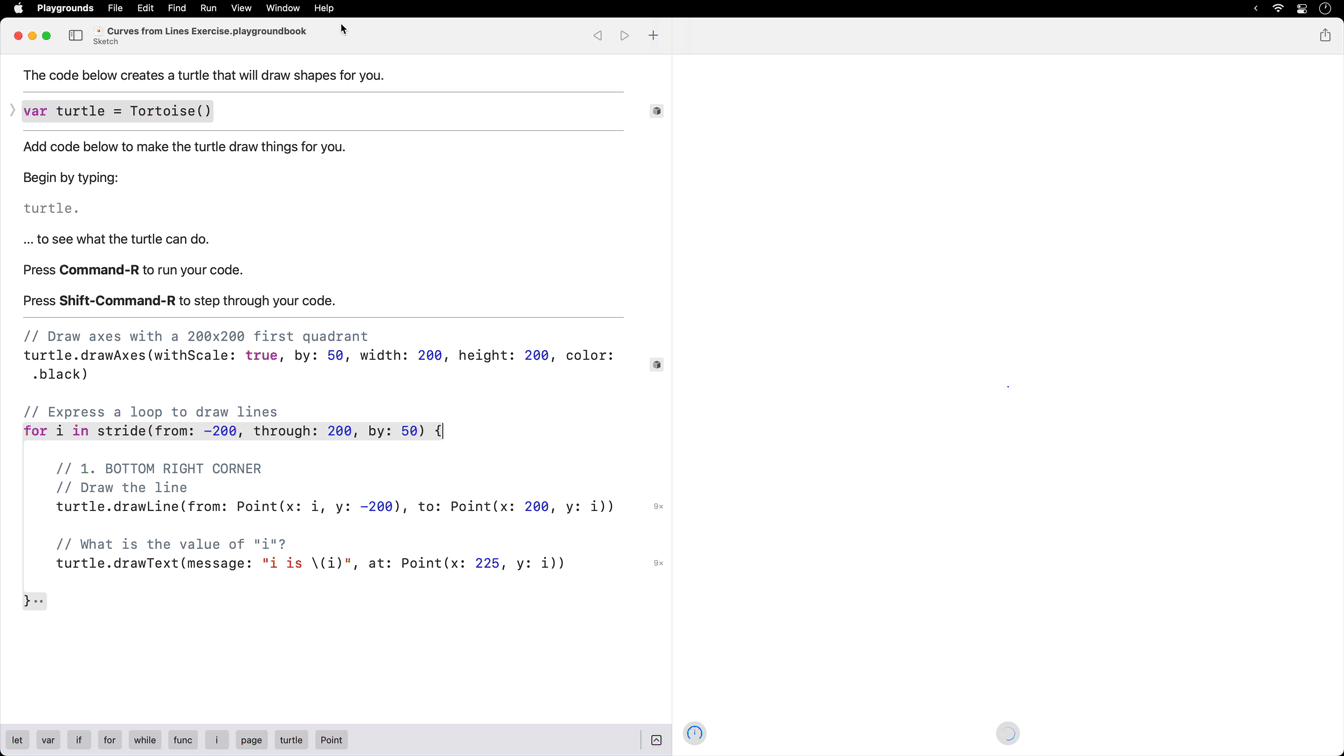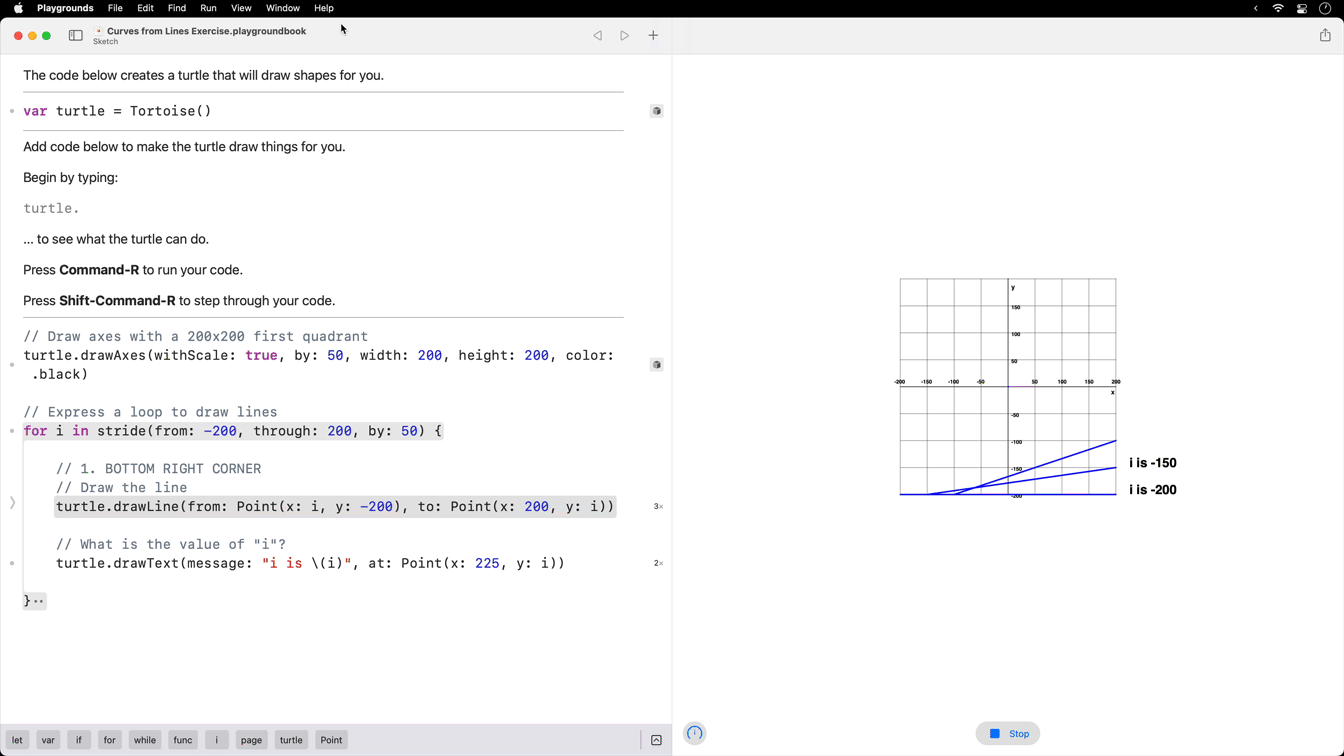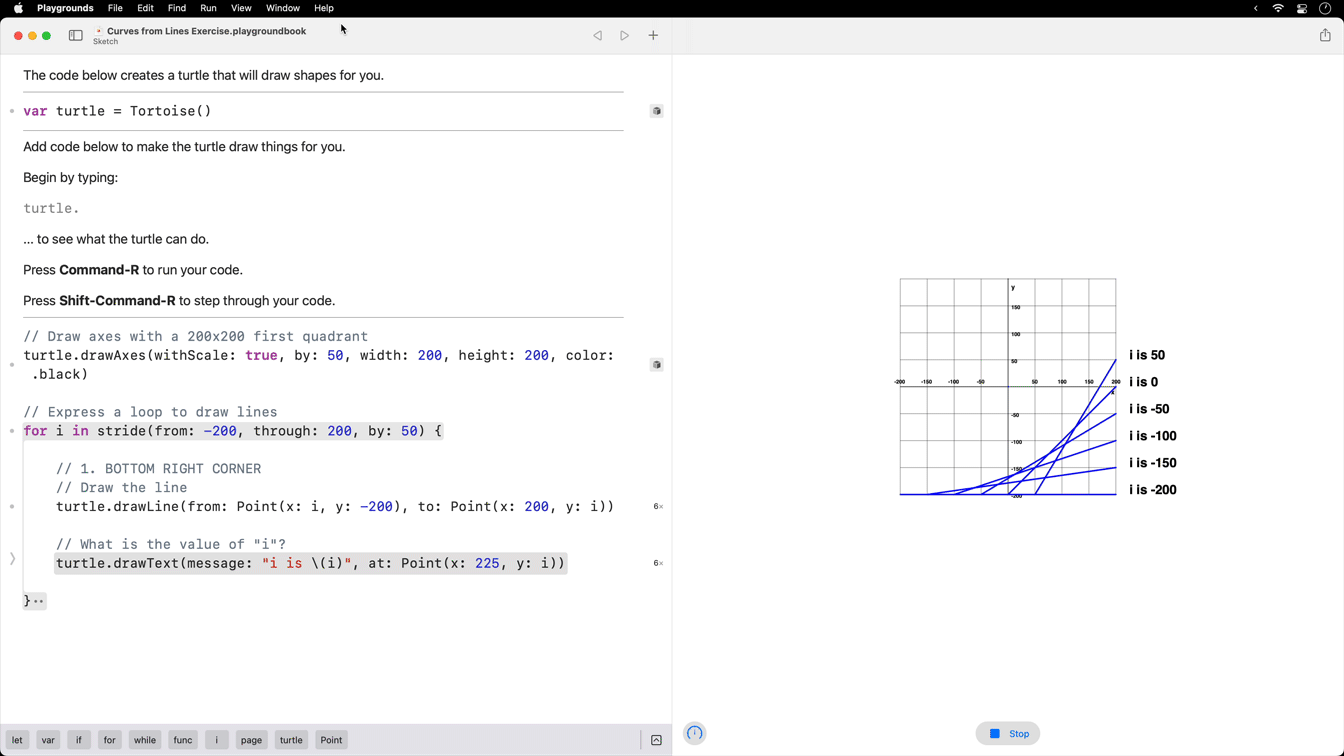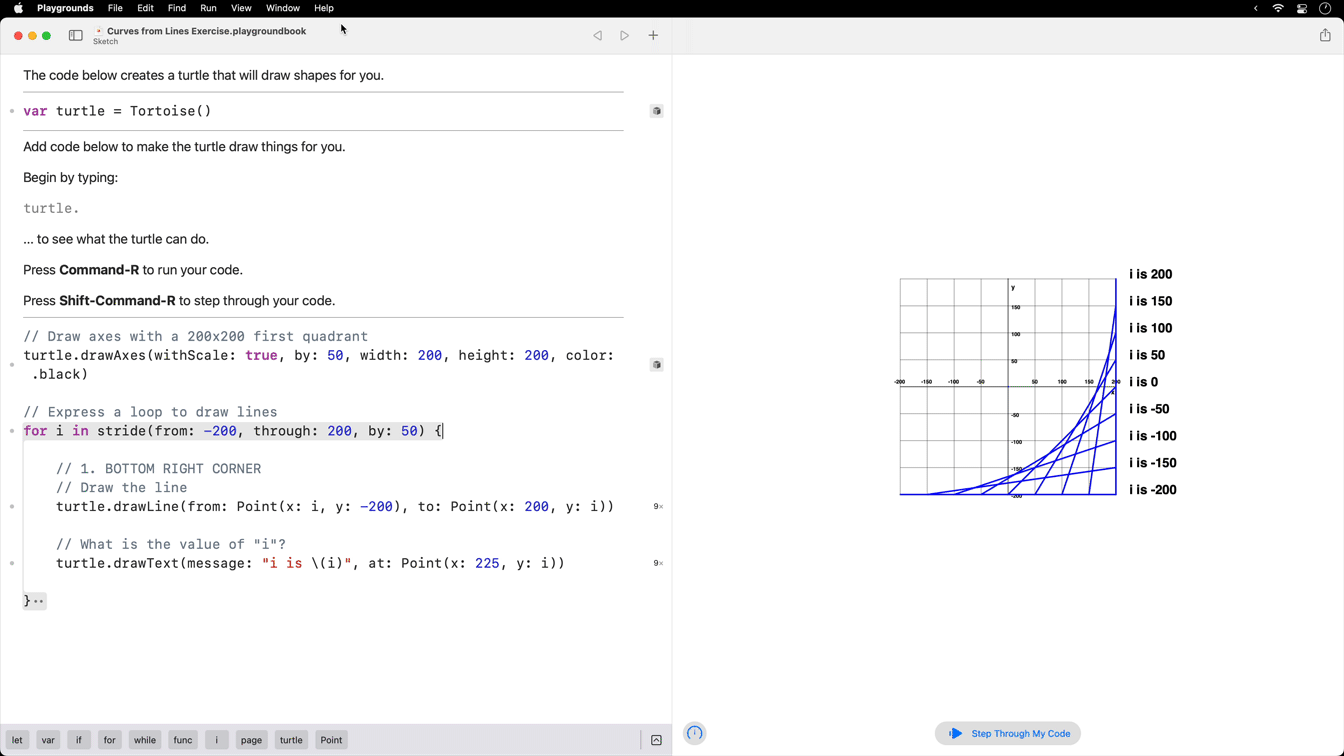
Here is what the code looks like:

The variable i holds the numerical value that changes.

We use i for the $x$ position of the from point and for the $y$ position of the to point.

The code above will produce the following result:

Exercises

1. Continue building out your plan so that you spot the patterns in the $x$ and $y$ values for the from and to points needed to draw the red lines shown here: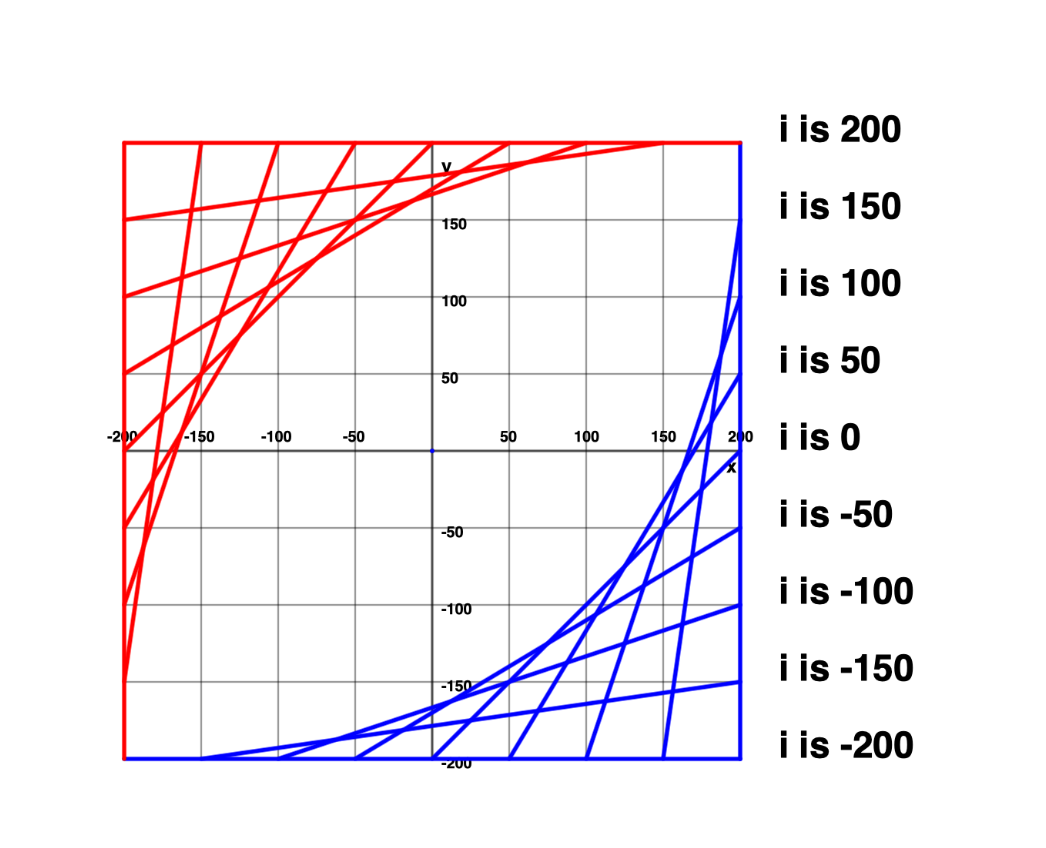

   

2. Make further additions to your plan and spot patterns in $x$ and $y$ values to draw the next corner of the design: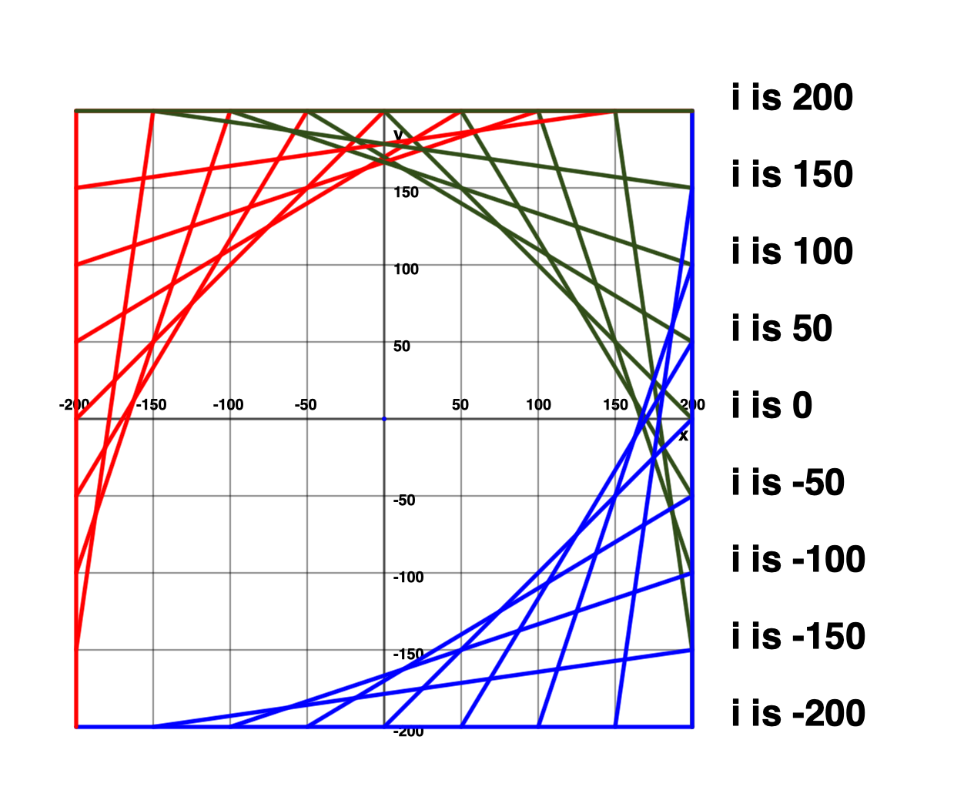

   

   Hint

   It may be helpful to consider a mathematical expression involving addition, subtraction, multiplication, or division that would let you use the existing loop to draw the green lines.

3. Finally, make changes to your plan and code to express the final corner of lines, shown here in purple: